During the processing stage, increased monitoring of foodstuffs can help in determining the quality attributes in real time and thus enable enhanced process control.
In a majority of process applications, the efficiency of a process and the quality of the end product is a function of the fluid’s rheology, which will affect several characteristics like spreadability, pourability, and pumpability (Cullen, Duffy & O’Donnell, 2001).
Conventionally, quality control rheological measurements have been performed on tomato-based products, both off-line and intermittently, using simple dip-in viscometers like the Brookfield viscometer (Barnes, 2001) and instruments like the Bostwick Consistometer (Cullen, Duffy & O’Donnell, 2001). The simple, cost-effective instrument — Bostwick Consistometer (BC) — is used for monitoring product consistency in an array of foodstuffs.
Yet, this instrument has certain imitations like dryness and leveling of the instrument, operator subjectivity and variability, and separation of serums at the edge of product flow. As a result, this device is not appropriate for on-line consistency measurements. Moreover, laboratory viscometers are extensively utilized as quality control instruments predicated on simple rotational viscometry, with shear rate reliant on the rotation speed and the type of spindle used. Therefore, substituting the Bostwick Consistometer and laboratory viscometers, or associating their measurements to a process viscometer, can offer real-time and continuous monitoring at the time of processing.
For process control, a wide range of viscometers are available such as vibrational, rotational, and tube viscometers, and also the appropriateness of such methods have been recently assessed for the food sector (Cullen et al. 2000). However, such kinds of traditional viscometer designs can be challenging when handling complex food fluids (particulate, fibrous, multiphase, and highly viscous), which leads to errors as a result of wall slip, fouling of measuring gap, or phase separation. An ideal viscometer design is one that enables a rapid response time, eases the cleaning process in place with least possibilities of fouling, and allows excellent sample renewal to make sure that any kind of measurement achieved is representative.
Various unit operations in the sector need effective mixing or mechanical agitation of fluids. In addition, the shape and size of the agitator used will be dependent on the properties — especially viscosity — of the fluid to be combined. For highly viscous non-Newtonian fluids, helical ribbon agitators are generally utilized, enabling vertical mixing of the fluid and efficient mixing at the vessel wall (Rai, Devotta, and Rao, 2000), with operating speeds usually within the range of 30–100 rpm. Improved process control can be achieved through in-situ rheological assessment of batches, before pumping and post-mixing.
Advantages include the elimination of the need for bypass processing lines or extra instrumentation to be in contact with the product combined with real-time monitoring. The use of mixer viscometry, in which high-precision measurements of impeller rotational speed and torque for a specified geometry can establish the obvious viscosity in the mixing vessel, has been documented well (Cantu-Lozano, Rao, and Gasparetto 2000; Ford and Steffe 1986).
Yet, trials like these are based on scale-down mixing geometries, depending on conventional off-line viscometer/rheometer measurement of speed and torque (Cullen, et al. 2000). Owing to the intricate flow patterns, and thus shear rates, in the mixing vessels, only average values and approximate data can be established (Castell-Perez and Steffe, 1992). The fabrication of a new, cost-effective non-contact torque transducer (TorqSense, Sensor Technology Ltd, Banbury, Oxon, UK) offering accurate dynamic measurements of rotary torque across ranges covering 0–10 mN⋅m to 0–10,000 N⋅m will support technology transfer of mixer viscometry to the production scale.
With regards to this torque transducer, the principle of operation involves a surface acoustic wave device, utilized as a frequency-dependent strain gauge, which determines the change in resonant frequency induced by the applied strain in the shaft. Also recorded was the precise measurement of shaft rotational speed utilizing a light beam.
The aim of this article was to assess the capability of a pilot plant-scale helical ribbon mixer as a rheological process control method, applying the below criteria:
- Establish effective power-law indices from representative mixer flow curves
- Establish power-law indices utilizing the mixer viscometer method
- Develop correlations between off-line reference methods and single-point mixer torque measurements
Materials and Methods
First, a pilot scale helical ribbon agitator (42 L) was developed that contains a cylindrical dished-bottom stainless steel vessel integrating a close clearance helical ribbon impeller, the geometrical configurations of which are illustrated in Figure 1 and listed in Table 1.
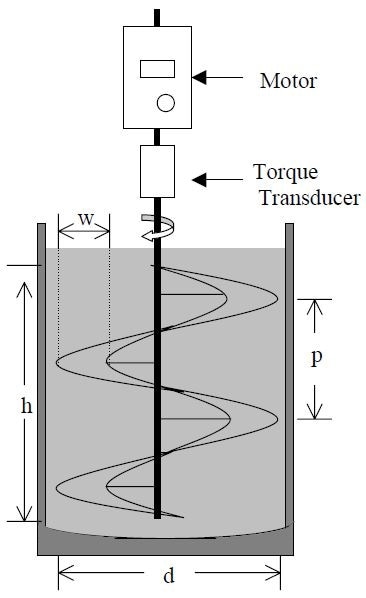
Figure 1. Schematic of pilot plant helical ribbon agitator
Table 1. Geometrical characteristics of helical ribbon agitator
| Parameter |
|
| Diameter, d (m) |
0.36 |
| Height, h (m) |
0.31 |
| Pitch, p (m) |
0.18 |
| Blade width, w (m) |
0.05 |
| Clearance, c (m) |
0.01 |
| p/d |
0.5 |
| c/d |
0.027 |
Both speed and torque were determined using a non-contact rotary torque transducer (Torqsense, Sensor Technology Ltd, Banbury, Oxon, UK) in the 0–6 N⋅m range and logged with the system software and transducer interface module. Then, using a variable speed Heidolph (model RZR 2041) stirrer motor (AGB Scientific Ltd, Dublin), the agitator speed was varied from 35 to 70 rpm. For each sample, the temperature was determined in the agitator and replicated on the rheometer.
Non-Newtonian fluids and Newtonian fluids (see Table 2) were used to establish the agitator’s mixer viscometer constant using the slope technique. Next, well-defined model fluids (Sigma-Aldrich Ireland Ltd, Dublin) were selected that span the spectrum of flow behavioral indices. To study the impacts of elasticity on torque, xanthan gum aqueous solutions (1%, 1.5%, and 2%) were employed as model fluids.
Table 2. Flow characteristics of standard fluids, as determined by laboratory rheometer
| Fluid |
K |
n |
| Pa.sn |
- |
| Glycerol |
5.55 |
0.98 |
| Glycerol / H2O / 0.1% CMCa |
8.66 |
0.68 |
| 0.5% Carboxymethyl cellulose |
10.3 |
0.56 |
| 1.0% Carboxymethyl cellulose |
25.5 |
0.49 |
| 1.5% Carboxymethyl cellulose |
65.6 |
0.43 |
| 0.5% Guar gum |
25.4 |
0.33 |
| 1.0% Guar gum |
80.9 |
0.25 |
| 1.5% Guar gum |
253.3 |
0.16 |
a85% mass glycerol, 15% mass water, 0.1% mass carboxymethylcellulose
The thickness of a commercial ketchup was increased by adding samples and tomato paste with different inconsistency from Bostwick values of ca. 2.5 to 10.5, by dilution. Then, a pizza sauce containing particulates of around 5.0 mm in length (Green Isle Foods, Naas, Ireland) was chosen as a fluid exhibiting more complex properties and differed in consistency across an insignificant range of Bostwick values from ca. 4.0 to 6.0, by dilution.
To achieve dilution levels, water quantities of ca. 1.5% of the total sample volume were added. Before measurement, these samples were combined at 20 °C for a period of 30 minutes. The ensuing mechanically degraded samples, replicating post-mixing conditions, were believed to be time-independent and eventually modeled as power-law fluids.
For every dilution with a Bostwick Consistometer (Christison Scientific, Gateshead, Tyne, and Ware, UK), off-line consistency measurements were taken, with values being taken as the distance in centimeters traveled by the sauce in a span of 30 seconds. On a laboratory rheometer, (Carrimed CSL2100, TA Instruments, Leatherhead, Surrey, UK), shear rate sweeps (0–300 second−1) were carried out using a parallel plate geometry (4 cm and 1500 μm gap) for samples of pizza sauce, and a cone and plate geometry (4 cm and 2° acrylic cone) for samples of tomato ketchup, at batch temperatures. Rheometer and BC rheometer measurements (shear rate sweeps) were then carried out in triplicate and averaged for every dilution.
Results and Discussion
Mixer Viscometer Constant
Figure 2 shows a linear regression analysis of the semi-logarithmic plot of (1 − n) versus (P/KΩn+1d3) that provided an excellent measure of fit (R2 = 0.99); ks — the shear rate proportionality constant — was established from the slope of the line as 10. This constant was ascertained to be independent of angular velocity for speeds of 40, 50, 60, and 70 rpm with correspondingly high measures of fit.
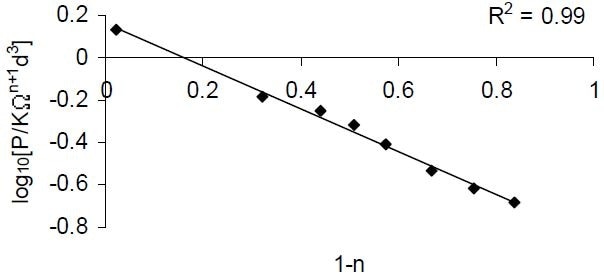
Figure 2. Semi-logarithmic plot of dimensionless functions (P/KΩn+1d3) versus (1 − n) for standard fluids as listed in Table 2.
Power-Law Indices
The flow behavioral index, established from the logarithmic plots of rotational speed versus mixer torque, yielded similar results to those determined with the laboratory rheometer, with an average percentage variation in magnitude of 5%. In addition, they defined the transition of the fluids tested toward more Newtonian behavior across a slight range of dilutions (see Figure 3). These outcomes demonstrate that agitators may be used to estimate the flow behavioral indices in situ, by determining torque as a function of rotational speed.
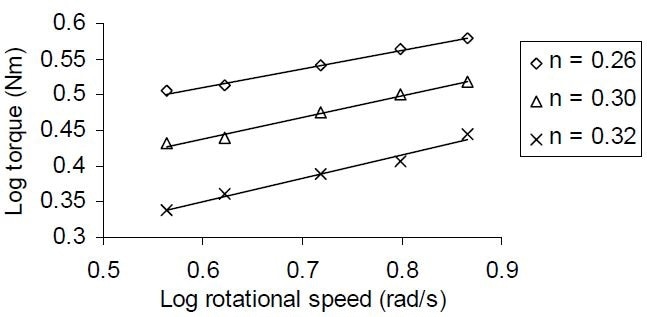
Figure 3. Logarithmic plot of torque versus rotational speed, for tomato ketchup samples.
The K values, established utilizing Equation (1) to their rheometer-quantified equivalents for a range of dilutions, are compared in Figure 4.
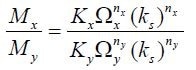 |
(1) |
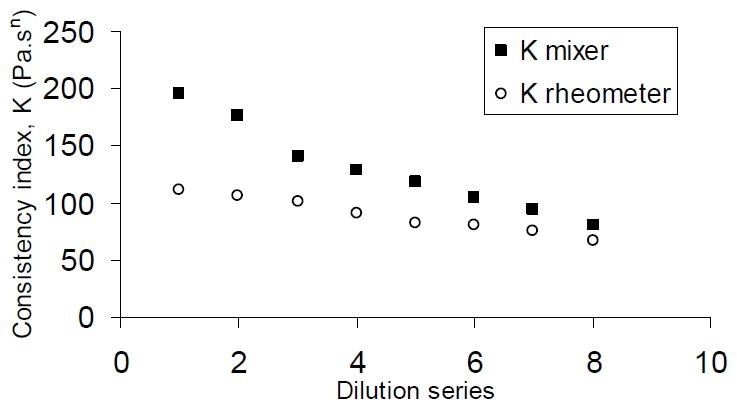
Figure 4. Consistency index (K) as determined by the mixer viscometer, compared to their rheometer-measured equivalents, for tomato ketchup samples (BC values 4.2–6.8).
The mixer viscometer provided significantly higher consistency index values, with the discrepancy inversely proportional to dilution. It is proposed that such a discrepancy is the result of the solid fraction of tomato products, leading to gel-like behavior or network structure (Rao and Cooley, 1992). In Figures 5, the viscoelastic behavior of a ketchup sample is examined, with G′ being higher than G″ at all frequencies (ω) determined. This indicates that the properties of the sample were more solid than viscous.
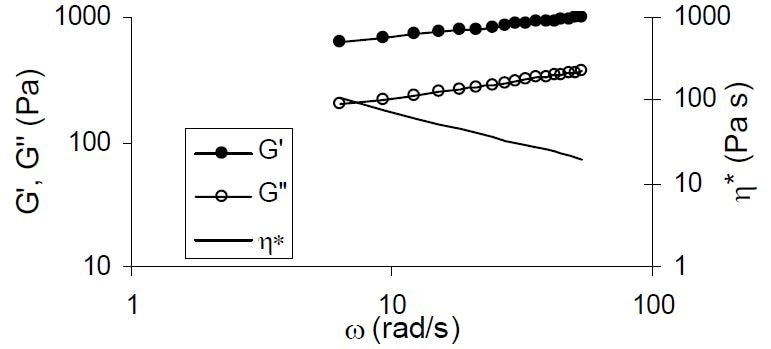
Figure 5. Logarithmic plot of angular frequency (ω) versus storage (G′) and loss (G″) moduli and η (η*) for a tomato ketchup sample.
The reduction in complex viscosity η* highlights the sample’s shear thinning nature. From a structural standpoint, log plots of G″ or G′ against log ω of weak gels produce true gels zero slopes and positive slopes. Therefore, it can be concluded that the tested tomato ketchup exhibited weak gel-like behavior. The impact of elasticity on combining with agitators including helical ribbons is vague, with numerous authors reporting increases, decreases, and no impacts on torque (Castell-Perez and Steffe, 1992). Conversely, elasticity is known to create variations in the flow fields around the mixing impeller, and usually, it is concluded that fluids’ elastic properties are inclined to reverse secondary flows caused by centrifugal force (Castell-Perez and Steffe, 1992).
Several authors, in this regard, have reported an evident increase in torque owing to elasticity for helical ribbons (Brito et.al. 1991; Collias and Prud’homme, 1985). A tripling of torque for certain fluids, as a result of elasticity, has also been reported by the latter authors. Thus, it can be surmised that this increased torque is not a function of the flow behavioral index or power-law consistency index.
To further assess this theory, xanthan gum — a well-defined reference fluid — was circulated in the helical ribbon agitator. The fluid has a gel-like structure at greater than 1.0% concentrations. The percentage variation in magnitude between the consistency index determined by the mixer viscometer and its equivalents measured by the rheometer increased from 3% at 1% concentrations to 7% and 50% at 1.5% and 2% concentrations, respectively. Therefore, the traditional method for non-Newtonian fluids devised by Metzner and Otto (1957) to establish power consumption in agitator systems does not consider the impacts of elasticity on torque created for complex fluids like tomato sauces. In a similar way, Equation (1) does not consider this effect as well.
Assessment studies performed on the impacts of elasticity on mixing involved the use of elastic fluids with a constant viscosity (Boger fluids). Considering the fact that a majority of viscoelastic fluids also have robust shear thinning properties, changes in power consumption could also be due to changes in either elasticity or viscosity (Castell-Perez and Steffe, 1992).
The generation of a correlation, which includes elasticity and also considers the variations in impeller geometry and viscosity, can pose challenges. From this work, it becomes apparent that the Otto and Metzner correlation may no longer be valid for scaling-up on the basis of power usage for each unit volume, as reported by Oliver et al. (1984), because of the different power needs owing to the changing fluid elasticity. The impacts of elasticity on quantified torque depend on scale, and this might explain as to why such effects are not found in the laboratory-scale studies described in the literature (Ford and Steffe, 1986; Castell-Perez and Steffe, 1992).
Representative Flow Curves
Effective viscosity as established through Equation (2) and then plotted against angular velocity was modeled as a power-law function. Figure 6 shows these representative flow curves for a set of dilutions for samples of tomato ketchup.
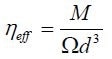 |
(2) |
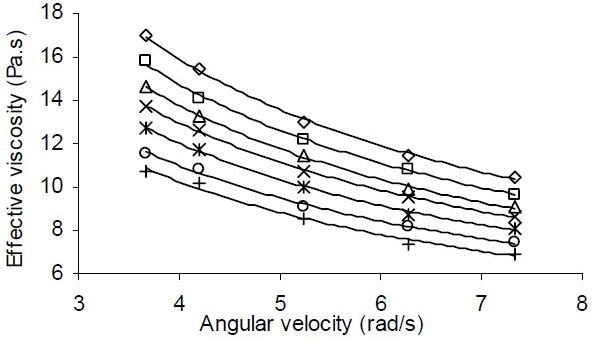
Figure 6. Representative flow curves of tomato ketchup samples for a series of dilutions (BC values 4.2–6.5).
Data regression analysis led to an effective flow behavioral index neff and an effective consistency coefficient Keff. Effective consistency was observed to correlate robustly (R2 = 0.99) against K determined by the rheometer (see Figure 7), indicating that the method could well be employed for process measurements of fluid consistency.
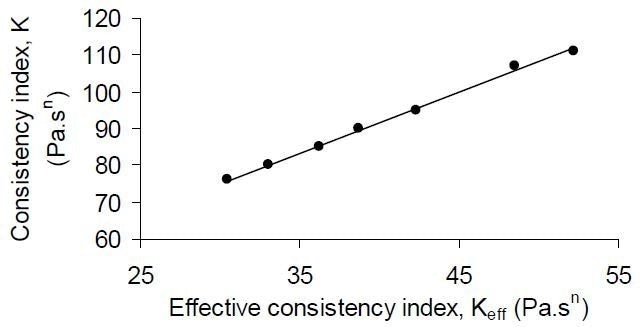
Figure 7. Linear correlation between effective consistency index (Keff), as determined from the mixer, against rheometer-measured consistency index values (K) for a series of dilutions of tomato ketchup samples (BC values 4.2–6.5).
Moreover, effective flow behavioral indices (neff) were numerically the same as those quantified above. In this method, one major benefit is that calibration model fluids are not needed. A flow curve is also generated for the product — instead of utilizing too many quality control procedures that could only give single-point measurements — leading to a more comprehensive rheological characterization. Effective consistency values strongly correlated (R2 = 0.97) against Bostwick Consistometer values.
Single-Point Measurements
From the agitator, raw torque data also correlated robustly (R2 = 0.98 and R2 = 0.99) with consistency index from the Bostwick and rheometer values, respectively utilizing a power-law model (see Figure 8).
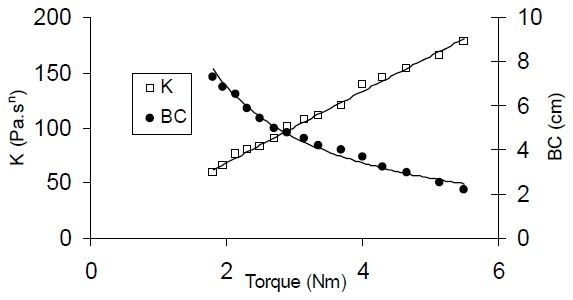
Figure 8. Correlations developed between off-line consistency index K (rheometer) and Bostwick values with torque measurements for a series of tomato ketchup sample dilutions.
Such high measures of fit combined with low standard errors of prediction (denoted as a percentage of the range), below 3% and 4% respectively, demonstrate that off-line reference measurement may be accurately predicted using torque readings at a constant speed. An analogously high measure of fit (R2 = 0.98) was achieved for the correlation created between the Bostwick values and torque readings for the samples of pizza sauce, across an extremely small consistency range, BC values 4.0–6.0 cm.
Furthermore, BC measurements were given in increments of 0.5 cm, the limit of the sensitivity of the instruments as stated by Cullen, Duffy, and O’Donnell (2001). The generation of a correlation with consistency coefficient, K, as established from rheometer shear rate sweeps, demonstrated to be more difficult, owing to the inability of the rheometer to handle samples comprising of large particulates, even utilizing the parallel plate geometry with a huge gap.
Additionally, the torque transducer was shown to be susceptible to insignificant variations in product consistency, which is characteristic of fluctuations in the sector and has the ability to handle large particulates. If several recipes or products have to be assessed, then it is better to develop such correlations for every particular product. Most often, quality control personnel are just interested in learning whether the product created is within the given range for daily production — the range created earlier based on the understanding of the entire flow curve (Barnes, 2001).
This quality control range — whether established by single viscosity readings from laboratory viscometers or consistometers — could be precisely predicted or substituted by mixer torque measurements, which also offers the advantages of real-time process monitoring.
Conclusions
Proposed mixer viscometry methods, combined with a new torque transducer, were assessed as a process control tool to track rheological characteristics of fluid foods in a helical ribbon agitator. Moreover, post-mixing rheological assessments of tomato-based products utilizing representative flow curves within a pilot plant scale helical ribbon agitator, demonstrated to be an effective method to achieve process viscometry measurements. Also, modeling effective viscosity as power-law functions yielded similar data to results measured by rheometer.
Developing correlations with steady speed torque measurements from the agitator can help predict reference off-line measurement methods. The torque transducer used was shown to be susceptible to even slight variations in product consistency. Comparison of torque readings utilizing Equation (1) to reference non-Newtonian fluid data failed to determine absolute power-law indices due to variations in elasticity. The effects of absolute power-law indices depend both on the viscoelastic properties of the fluid and the scale and geometry of operation.
Design benefits of the recommended viscometry system for the sector include its potential to handle the properties of complex fluid like fibers and particulates. Errors and subjectivity owing to operator variability, related to specific off-line instruments, are also eliminated. Real-time process monitoring enables enhanced process control. Moreover, rheological measurement issues caused by particle blockages or slip are not faced. Extra cleaning or instrumentation in contact with the foodstuff is no longer needed. It is recommended that other low-speed impeller designs, which function in the laminar flow region, like paddles and anchors, could also be utilized for other kinds of viscous fluids.
References
- Barnes, H.A. (2001). An examination of the use of rotational viscometers for the quality control of non-Newtonian liquid products in factories. Applied Rheology, 11, 89–101.
- Brito, E., Leuliet, J.C., Choplin, L. & Tanguy, P.A. (1991). On the role of elasticity on mixing with a helical ribbon impeller. Trans. I. Chem.E. 69, 324–331.
- Cantu-Lozano, D., Rao, M.A. & Gasparetto, C.A. (2000) Rheological properties of noncohesive apple dispersion with helical and vane impellers: effect of concentration and particle size. J. Food Process Eng. 23, 373–385.
- Castell-Perez, M.E. & Steffe, J.F. (1992). Using mixing to evaluate rheological properties. In M.A. Rao, & J.F. Steffe, Viscoelastic properties of foods (p. 247–284). London: Elsevier Applied Science.
- Collias, D.J. & Prud’homme, R.K. (1985). The effect of fluid elasticity on power consumption and mixing times in stirred tanks. Chem. Eng. Sci. 40(8), 1495–1505.
- Cullen, P.J., Duffy, A.P., O’Donnell, C.P. & O’Callaghan, D.J. (2000). Process viscometry for the food industry. Trends Food Sci. Technol., 11(12), 451–457.
- Cullen, P.J., Duffy, A.P., O’Donnell, C.P. (2001). On-line rheological characterization of pizza sauce using tube viscometry. J. Food Process Eng. 24 (3), 145–159.
- Ford, E.W. & Steffe, J.F. (1986). Quantifying thixotropy in starch-thickened, strained apricots using mixer viscometry techniques. J. Texture Studies, 17, 71–85.
- Metzner, A.B. & Otto, R.E. (1957). Agitation of non-Newtonian fluids, A.I.Ch.E.J. 3(1) 3–10.
- Oliver, D.R. Nienow, A.W. Mitson, R.J. & Terry, K. (1984). Power consumption in the mixing of Boger fluids. Chem. Engng. Res. Des., 62, 123–127.
- Rai, C.L., Devotta, I. & Rao, P.G. (2000). Heat transfer to viscous Newtonian and non-Newtonian fluids using a helical ribbon agitator. Chem. Eng. J. 79, 73–77.
- Rao, M.A. & Cooley, H.J. (1992). Rheological behaviour of tomato pastes in steady and dynamic shear. J. Texture Studies, 23, 415–425.
- Rieger, F & Novak, V. (1973). Power consumption of agitators in highly viscous non-Newtonian liquids. Trans. Instn. Chem. Engrs. 51, 105–111.
- Shamlou, P.A. & Edwards, M.F. (1985). Power consumption of helical ribbon mixers in viscous Newtonian and non-Newtonian fluids. Chem. Eng. Sci. 40(9), 1773–1781.
- Steffe, J.F. (1996) Rheological methods in food process engineering (2nd ed.). Michigan: Freeman Press.

This information has been sourced, reviewed and adapted from materials provided by Sensor Technology.
For more information on this source, please visit Sensor Technology.